What Are Bitwise Operators
Bitwise operators are operators that have an effect on bits in memory, most commonly used with numbers, such as integers. An unsigned 8 bit integer for example is stored in memory as a row of bits e.g. 0 is represented in memory as 00000000, 255 would be 11111111 and 123 would be 01000101. To represent a number in binary, you start from the right hand side and go towards the left, every step to the left signifies a 2^n value for that bit, where n equals the amount of steps taken towards the left. Bitwise operators can have an effect on the level of an individual bit. A common use case for these operators is working with bitflags.
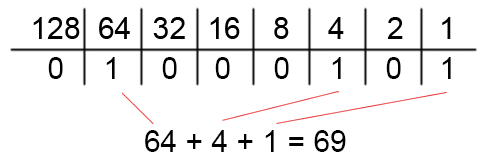
Types of Bitwise Operators
There’s 6 different bitwise operators in c++ (&, |, ~, ^, « and »), some of these might look similar but are not to be confused with the logical operators such as && or || which have very different results when used.
The AND Operator (&)
The & operator works in a similar way as the logical &&, but on a bit level instead of with booleans. Meaning if both of 2 numbers in the operation have that bit set to 1, the result will also have this bit set to one. A great usage of this is to check whether a number is even or by performing the x & 1 operation, if the result is 1 the number is odd, if the result is 0, the number is even.
A few examples with their binary breakdown:
1 & 255 = 1
00000001
& 11111111
= 0000001
148 & 45 = 4
10010100
& 00101101
= 00000100
157 & 150 = 148
10011101
& 10010110
= 10010100
The OR Operator (|)
The | operator is also very close to its logical lookalike ||, but again on the level of bits. This operator will set the resulting bit to one if either one of the input numbers has this bit set to 1.
A few examples:
1 | 255 = 255
00000001
| 11111111
= 11111111
148 | 45 = 189
10010100
| 00101101
= 10111101
157 | 150 = 159
10011101
| 10010110
= 10011111
The XOR Operator (^)
The ^ performs an exclusive or operation on the input bits, the resulting bit will be 1 of one of the inputs has the bit set to one BUT not the other. So if exclusively one of the input bits is 1, the result will be 1. If both input bits are 1 or both are 0, the result will be 0.
A few examples:
1 ^ 255 = 254
00000001
| 11111111
= 11111110
148 ^ 45 = 185
10010100
| 00101101
= 10111001
157 & 150 = 11
10011101
| 10010110
= 00001011
The NOT Operator (~)
The ~ operator is the only one of these that only takes one number as input. What this operator does is it inverts all the bits of the input, so if an input bit is set to 1, it will become 0 in the result and vice versa.
A few examples:
~1 = 254
~ 00000001
= 11111110
~148 = 107
~ 10010100
= 01101011
~157 = 98
~ 10011101
= 01100010
The Shift Operators (« and »)
These operators have very specific use cases. The operation takes the form of x « n, where x is the number you’re shifting and n is the amount you’re shifting it with. What this entails is that it simply moves all the bits n positions to the left for « and to the right for ». If any set bit “falls off” the amount of bits it is just gone and is no longer considered, any bits that get “inserted” from e.g. the right when doing a « operation will be set to 0. A fun trick to do with this for example is to shift everything 1 bit to the left to double a number or to the right to get half that number.
A few examples:
1 << 2 = 4
~ 00000001
= 00000100
148 >> 3 = 18
~ 10010100
= 00010010
157 << 7 = 128
~ 10011101
= 10000000